Minimum Cost Walk (MINWALK)
Consider a weighted, undirected and connected graph
with n nodes, numbered 1 to n, and m edges. Find the minimum cost of any walk from node s to node t, via node v (visiting node v is compulsory), where cost of a walk is the sum of
weights of distinct edges occurring in the walk. This means that even if an
edge occurs multiple times in a walk, its weight is added only once to the cost
of the walk.
Input. The first line contains the number of test
cases t. Then t test
cases follow.
The first line of each test case contains 2 space
seperated integers: n (1 ≤ n
≤ 105) and m (n – 1 ≤ m ≤ min(105, n
* (n – 1) / 2).
The next line contains 3 space seperated integers: s, t and v (1 ≤ s,
t, v ≤
n).
The next m lines contain 3 space seperated integers each: a b c (1 ≤ a, b
≤ n, 1 ≤ c ≤ 109), denoting an edge between nodes a and b with weight c.
Note: There is at most one edge between any pair of
nodes and there are no self loops.
Output. Output the required answer for each test case
on a separate line
|
Sample input |
Sample output |
|
2 4
3 1
3 4 1
2 1 2
3 2 2
4 3 4
3 1
1 4 1
2 1 2
3 2 2
4 3 |
6 4 |
РЕШЕНИЕ
графы – алгоритм Дейкстры
Задан
взвешенный граф из n вершин. Найдите стоимость пути из вершины s в t, посетив обязательно при этом вершину v. Стоимость каждого ребра следует
считать только один раз (даже если по ребру придется пройти дважды).
Анализ алгоритма
Рассмотрим
путь из s в
t, проходящий
через v. Тогда существует такая вершина u, что путь
имеет вид: s → u → v → u → t. То есть путь от u до v и от v до u идет по тем же самым ребрам. Если путь по каждому ребру проходит только один раз, то
можно считать что u совпадает
с v.
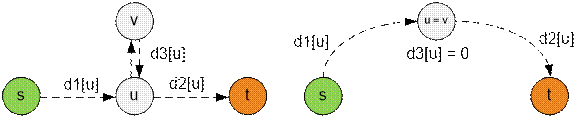
Запустим
алгоритм Дейкстры из вершин s, t, v. Пусть
d1[u], d2[u], d3[u] – соответственно величины кратчайших путей от s, t, v до u. Остается
перебрать все возможные значения u (1 ≤ u ≤ n) и найти такое u, что d1[u] + d2[u] + d3[u] минимально.
Реализация алгоритма
#include <cstdio>
#include <vector>
#include <queue>
#define INF 0x3F3F3F3F3F3F3F3FLL
using namespace std;
long long min(long long a, long long b)
{
return (a < b) ? a : b;
}
struct edge
{
int node;
long long dist;
edge(int node, long long dist) :
node(node), dist(dist) {}
};
bool operator< (edge a,
edge b)
{
return a.dist > b.dist;
}
vector<vector<edge>
> g;
void Dijkstra(vector<vector<edge> >
&g, vector<long long> &d,
int start)
{
priority_queue<edge>
pq;
pq.push(edge(start,
0));
d = vector<long long>(g.size(), INF);
d[start] = 0;
while (!pq.empty())
{
edge e =
pq.top(); pq.pop();
int v = e.node;
if (e.dist > d[v]) continue;
for (int j = 0; j <
g[v].size(); j++)
{
int to = g[v][j].node;
int cost = g[v][j].dist;
if (d[v] + cost < d[to])
{
d[to] = d[v] +
cost;
pq.push(edge(to,
d[to]));
}
}
}
}
int tests, n, m;
int s, t, v, v1, v2;
long long cost;
int main()
{
scanf("%d", &tests);
while (tests--)
{
scanf("%d %d", &n, &m);
g.clear();
g.resize(n + 1);
scanf("%d %d %d", &s, &t, &v);
for (int i = 0; i <
m; i++)
{
scanf("%d %d %lld", &v1, &v2, &cost);
g[v1].push_back(edge(v2,
cost));
g[v2].push_back(edge(v1,
cost));
}
vector<long long> d1, d2, d3;
Dijkstra(g, d1,
s);
Dijkstra(g, d2,
t);
Dijkstra(g, d3,
v);
long long res = 1e18;
for (int u = 1; u <=
n; u++)
res = min(d1[u]
+ d2[u] + d3[u], res);
printf("%lld\n", res);
}
return 0;
}